0属于{0},空集不属于{0}。因为{0}中不含有元素“空集”,正确的说法应该是“空集⊆{0}”或者“空集⊂{0}”0属于{0}。
不含任何元素的集合。空集是任何集合的子集,是任何非空集合的真子集。空集不是无;它是内部没有元素的集合。可以将集合想象成一个装有元素的袋子,而空集的袋子是空的,但袋子本身确实是存在的。
基础概念
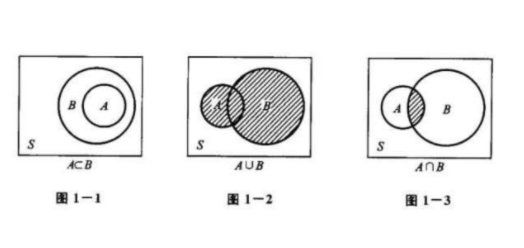
集合论是从一个物件o和集合A之间的二元关系开始:若o是A的元素,可表示为o ∈ A。由于集合也是一个物件,因此上述关系也可以用在集合和集合的关系。另外一种二个集合之间的关系,称为包含关系。
若集合A中的所有元素都是集合B中的元素,则称集合A为B的子集,符号为A ⊆ B。例如{1,2}是{1,2,3}的子集,但{1,4}就不是{1,2,3}的子集。依照定义,任一个集合也是本身的子集,不考虑本身的子集称为真子集。集合A为集合B的真子集当且仅当集合A为集合B的子集,且集合B不是集合A的子集。


